一直使用python实现一些想法，近期在使用python的过程中出现这样一个需求，定义了一个函数。第一个是普通參数。第二个是默认參数，后面还有可变參数，在最初学习python的时候，都知道非keyword可变參数和keyword可变參数两种，调用的方式或许多种多样，这里主要提出一个比較隐含的问题。并将各种可能出现的情况进行了探讨。

函数声明格式

python尽管不支持函数重载，可是通过对函数參数的众多特性的支持基本弥补了。

函数声明的通式例如以下：

def func(argv1,argv2...[,argv_d = default1,...]\        [,*var_argv][,**var_key_argv])

这是python函数声明的通式。首先是普通參数若干个。也能够没有，接着是带默认值的參数。然后是非keyword可变參数，最后是keyword可变參数。这为python提供的强大函数调用奠定了基础。

函数调用

正是在函数调用的过程中遇到了问题。为了说明。我定义了一个例如以下的函数进行说明：

def f1(a,b=1,*var): print a,'\t',b,'\t',vardef f2(a,b=1,**var): print a,'\t',v,'\t',var

首先普通參数能够使用按位置的方式调用，同一时候能够使用按形參keyword调用。默认值參数也是使用位置方式匹配或者keyword调用。实比例如以下：

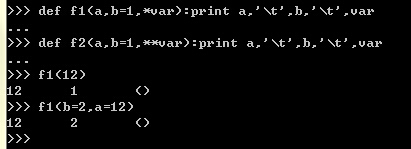这里没有使用后面的可变參数。一切都没有问题。

问题是。本人遇到的一个需求是，默认參数须要就是使用默认值调用。同一时候还有可变參数，并且是非keyword參数，那么调用时就会出现以下的情况：

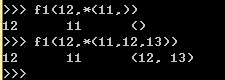能够看到，通过非keyword可变參数传入參数之后。python会默认把非keyword可变參数的前面若干个（这里是1个）当做默认參数，这里是由于我没有提供默认參数b的值，正是这个原因，在我的程序中一直没发现。

后来自习思考一下。发现Python解释器做出这种决定还是有一定的道理的，由于非keyword可变參数是默认參数之后的若干个參数。而在调用的时候由于没有传入默认參数的值。Python无法推断究竟从哪里開始是可变參数，因此在没有传入默认參数的值时，就依次从非keyword參数（调用者觉得的）中依照顺序抽取去当做默认參数的值，这从側面论证了非keyword可变參数在python内部是和普通參数默认參数一并处理的。

尽管上述调用有些极端，可是确实会出现这种需求，那么能够使用keyword可变參数进行替换，上述问题就能够攻克了，由于解释器是能够差别keyword參数和默认參数的，调用例如以下：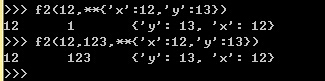

在使用keyword可变參数时，另一个重要问题就是，keyword參数的键值不能有普通參数或者默认參数的參数名反复，这从側面论证了，python对keyword调用和keyword可变參数在内部都是经过同一个字典保存的，因此不能有反复的键。调用例如以下：

上述遇到的问题是在实际操作过程中遇到的，一般从各种教程、书本学习python都仅仅是说明上述的函数声明和调用的方式。可是差点儿没有这种实际操作中可能遇到的点点滴滴，因此学习不论什么东西最好的方式就动手，这个真理永远不会变啦！